二叉搜索树
2022/2/20 treeheap
# Tree基本结构
function BinaryTree(data, left, right) {
this.data = data; // 节点的值
this.left = left; // 左节点
this.right = right; // 右节点
}
function BST() {
this.root = null;
}
/**
* 定义插入属性
* @param key int|float 要插入的值
*/
BST.prototype.insert = function(data) {
var newNode = new BinaryTree(data, null, null);
// 如果没有root节点
if (this.root === null) {
this.root = newNode;
} else {
this.insertNode(this.root, newNode);
}
};
/**
* 插入数据 left小 ,right大
* @param node obj 节点数据
* @param newNode obj 要插入的节点数据
*/
BST.prototype.insertNode = function(node, newNode) {
if (newNode.data < node.data) {
if (node.left === null) {
node.left = newNode;
} else {
this.insertNode(node.left, newNode);
}
} else {
if (node.right === null) {
node.right = newNode;
} else {
this.insertNode(node.right, newNode);
}
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
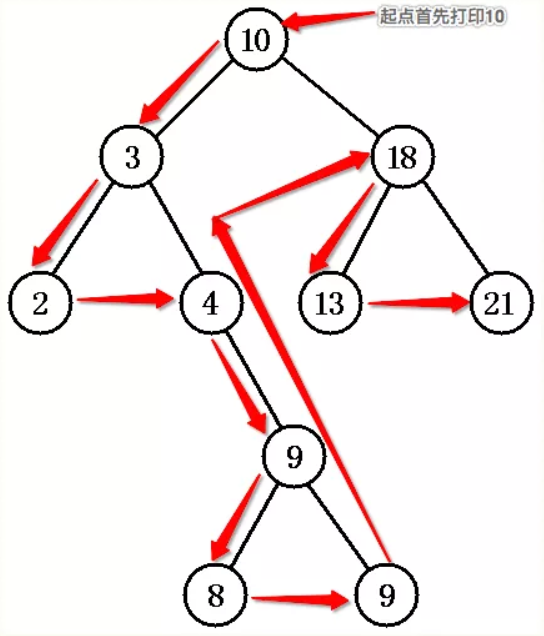
# 前序排列查询
val -> 左 -> 右
示例图
![20200102225235]()
递归实现
/**
* 前序查询
* @param node obj 节点
* @returns {Array}
*/
BST.prototype.preOrder = function(node) {
var nodeArr = [];
var node = this.root;
if (node !== null) {
this.preOrderNode(node, nodeArr);
}
return nodeArr;
};
/**
* 前序(中->左->右)
* @param node obj 节点
* @param nodeArr 存储查询的值
*/
BST.prototype.preOrderNode = function(node, nodeArr) {
if (node !== null) {
nodeArr.push(node.data); // <- there
this.preOrderNode(node.left, nodeArr);
this.preOrderNode(node.right, nodeArr);
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
var preOrderNode = function(root) {
let result = []
if(!root) return result
const stack = [] // 栈结构
stack.push(root)
while(stack.length){
const cur = stack.pop();
result.push(cur.val)
// 若栈顶结点有右孩子,则将右孩子入栈
if(cur.right){
stack.push(cur.right)
}
// 若栈顶结点有左孩子,则将左孩子入栈
if(cur.left){
stack.push(cur.left)
}
}
return result
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
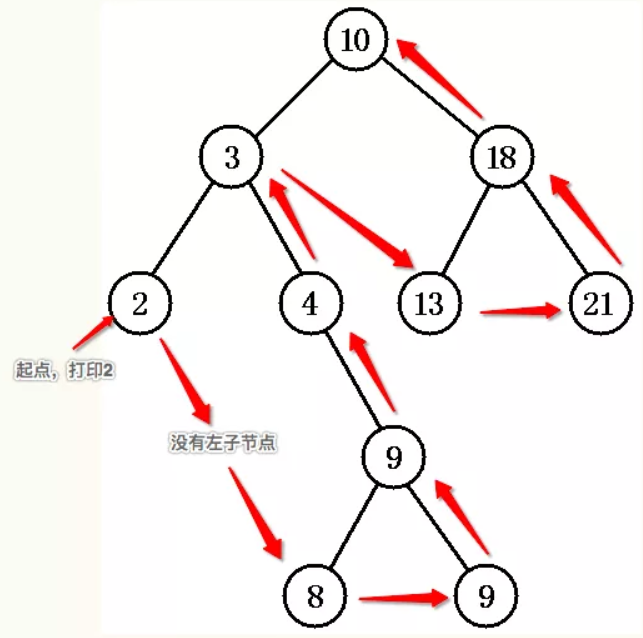
# 中序排列查询
左 -> val -> 右
示例图
![20200102225508]()
递归实现
/**
* 中序排列查询
* @param node obj 节点
* @returns {Array}
*/
BST.prototype.inOrder = function(sort = "ASC") {
var nodeArr = [];
var node = this.root;
if (node !== null) {
if (sort.toUpperCase() == "DESC") {
this.inOrderDescNode(node, nodeArr);
} else {
this.inOrderAscNode(node, nodeArr);
}
}
return nodeArr;
};
/**
* 中序查询-升序(左->中->右)
* @param node obj 节点
* @param nodeArr array 存储排序的值
*/
BST.prototype.inOrderAscNode = function(node, nodeArr) {
if (node !== null) {
this.inOrderAscNode(node.left, nodeArr);
nodeArr.push(node.data); // <- there
this.inOrderAscNode(node.right, nodeArr);
}
};
/**
* 中序查询-降序(右->中->左)
* @param node obj 节点
* @param nodeArr array 存储排序的值
*/
BST.prototype.inOrderDescNode = function(node, nodeArr) {
if (node !== null) {
this.inOrderDescNode(node.right, nodeArr);
nodeArr.push(node.data); // <- there
this.inOrderDescNode(node.left, nodeArr);
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
const inorderTraversal = function(root) {
// 定义结果数组
const res = []
// 初始化栈结构
const stack = []
// 用一个 cur 结点充当游标
let cur = root
// 当 cur 不为空、或者 stack 不为空时,重复以下逻辑
while(cur || stack.length) {
// 这个 while 的作用是把寻找最左叶子结点的过程中,途径的所有结点都记录下来
while(cur) {
// 将途径的结点入栈
stack.push(cur)
// 继续搜索当前结点的左孩子
cur = cur.left
}
// 取出栈顶元素
cur = stack.pop()
// 将栈顶元素入栈
res.push(cur.val)
// 尝试读取 cur 结点的右孩子
cur = cur.right
}
// 返回结果数组
return res
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
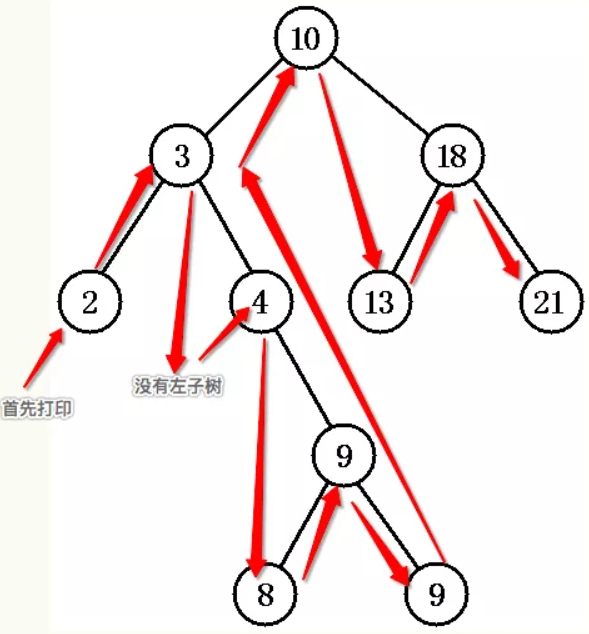
# 后序排列查询
左 -> 右 -> val
示例图
![20200102225635]()
递归实现
/**
* 后序查询
* @param node obj 节点
* @returns {Array}
*/
BST.prototype.reOrder = function(node) {
var nodeArr = [];
var node = this.root;
if (node !== null) {
this.reOrderNode(node, nodeArr);
}
return nodeArr;
};
/**
* 后序(左->右->中)
* @param node obj 节点
* @param nodeArr 存储查询的值
*/
BST.prototype.reOrderNode = function(node, nodeArr) {
if (node !== null) {
this.reOrderNode(node.left, nodeArr);
this.reOrderNode(node.right, nodeArr);
nodeArr.push(node.data); // <- there
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
const postOrder = function(root) {
// 定义结果数组
const res = []
// 处理边界条件
if(!root) {
return res
}
// 初始化栈结构
const stack = []
// 首先将根结点入栈
stack.push(root)
// 若栈不为空,则重复出栈、入栈操作
while(stack.length) {
// 将栈顶结点记为当前结点
const cur = stack.pop()
// 当前结点就是当前子树的根结点,把这个结点放在结果数组的(头部)
res.unshift(cur.val) //
// 若当前子树根结点有左孩子,则将左孩子入栈
if(cur.left) {
stack.push(cur.left)
}
// 若当前子树根结点有右孩子,则将右孩子入栈
if(cur.right) {
stack.push(cur.right)
}
}
// 返回结果数组
return res
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 最大值
BST.prototype.max = function(node) {
var node = this.root;
var newNode = this.maxNode(node);
return newNode === null ? null : newNode.data;
};
BST.prototype.maxNode = function(node) {
if (node === null) return null;
while (node !== null && node.right !== null) {
node = node.right;
}
return node;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
# 最小值
BST.prototype.min = function(node) {
var node = this.root;
var newNode = this.minNode(node);
return newNode === null ? null : newNode.data;
};
BST.prototype.minNode = function(node) {
if (node === null) return null;
if (node.left !== null) return this.minNode(node.left);
return node;
};
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
# 查询节点
BST.prototype.searchNode = function(node, data) {
if (node === null) {
return false;
}
if (data < node.data) {
return this.searchNode(node.left, data);
} else if (data > node.data) {
return this.searchNode(node.right, data);
} else {
return true;
}
};
BST.prototype.search = function(data) {
return this.searchNode(this.root, data);
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 移除节点
/**
* 移除一个节点
* @param data int|float 要移除的节点值
* @param node obj 节点
* @returns {*}
*/
BST.prototype.remove = function(data) {
var node = this.root;
return this.removeNode(node, data);
};
/**
* 移除节点
* @param data int|float 要移除的节点值
* @param node obj 节点
* @returns {*}
*/
BST.prototype.removeNode = function(node, data) {
if (node === null) return null;
if (data < node.data) {
node.left = this.removeNode(node.left, data);
return node;
} else if (data > node.data) {
node.right = this.removeNode(node.right, data);
return node;
} else {
// 这事判断第一种情况,没有左右分支的情况下,
if (node.left === null && node.right === null) {
node = null;
return node;
}
// 这是左子树为空的情况
if (node.left === null) {
node = node.right;
return node;
} else if (node.right === null) {
// 这是右子树为空的情况
node = node.left;
return node;
} else {
// 如果左右两个分支都存在的时候
// 寻找该节点的右节点的最小节点
var aux = this.minNode(node.right);
// 将改节点与找到的最小节点值互换
node.data = aux.data;
// 删掉替换后的最小节点
node.right = this.removeNode(node.right, aux.data);
return node;
}
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# 广度优先
- 层序遍历
function BFS(root) {
const queue = [] // 初始化队列queue
// 根结点首先入队
queue.push(root)
// 队列不为空,说明没有遍历完全
while(queue.length) {
const top = queue[0] // 取出队头元素
// 访问 top
console.log(top.val)
// 如果左子树存在,左子树入队
if(top.left) {
queue.push(top.left)
}
// 如果右子树存在,右子树入队
if(top.right) {
queue.push(top.right)
}
queue.shift() // 访问完毕,队头元素出队
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 翻转二叉树
var invertTree = function(root) {
if(!root) return root
let left = invertTree(root.left)
let right = invertTree(root.right)
root.left = right;
root.right = left
return root
}
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
# 相同的树
var isSameTree = function(p, q) {
if(p ==null && q == null) return true
if(p == null || q == null) return false
if(p.val != q.val) return false
// 分别比较左子树 和 右子树
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right)
};
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
# 其他方法
// 求二叉树节点个数
const sizeOfNode = function(node) {
if (!node) {
return 0;
}
return 1 + sizeOfNode(node.left) + sizeOfNode(node.right);
};
// 求二叉树层级
const levelOfNode = function(node) {
if (!node) {
return 0;
}
return (
Math.max(levelOfNode(node.left), levelOfNode(node.right)) + 1
);
};
// 求二叉树第K层的节点个数
const numKLevel = function(node, k) {
if (k < 0) {
return 0;
}
if (node === null) {
return 0;
}
if (node !== null && k === 1) {
return 1;
}
return numKLevel(node.left, k - 1) + numKLevel(node.right, k - 1);
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Trie (前缀树)
前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查
var Trie = function() {
this.children = {}
};
/**
* @param {string} word
* @return {void}
*/
Trie.prototype.insert = function(word) {
let node = this.children
for(const ch of word){
if(!node[ch]){
node[ch]={}
}
node = node[ch]
}
node.isEnd = true
};
Trie.prototype.searchPrefix = function(word) {
let node = this.children
for(const ch of word){
if(!node[ch]) {
return false
}
node = node[ch]
}
return node
};
/**
* @param {string} word
* @return {boolean}
*/
Trie.prototype.search = function(word) {
const node = this.searchPrefix(word)
return node !== undefined && node.isEnd != undefined
};
/**
* @param {string} prefix
* @return {boolean}
*/
Trie.prototype.startsWith = function(prefix) {
return this.searchPrefix(prefix)
};
/**
* Your Trie object will be instantiated and called as such:
* var obj = new Trie()
* obj.insert(word)
* var param_2 = obj.search(word)
* var param_3 = obj.startsWith(prefix)
*/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
# 将有序数组转换为二叉搜索树
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} nums
* @return {TreeNode}
*/
var sortedArrayToBST = function(nums) {
if(nums.length == 0) return null;
return dfs(nums, 0, nums.length-1)
};
function dfs(nums, left, right){
if(left > right){
return null
}
let mid = Math.floor(left + (right - left) / 2);
let root = new TreeNode(nums[mid])
root.left = dfs(nums, left, mid -1)
root.right = dfs(nums, mid+1, right)
return root
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 最小堆与最大堆(heap)
来源:学习javascript数据结构与算法(第三版)
- util.js
export const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1,
EQUALS: 0
};
export function defaultCompare(a, b) {
if (a === b) {
return Compare.EQUALS;
}
return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
export function swap(array, a, b) {
/* const temp = array[a];
array[a] = array[b];
array[b] = temp; */
[array[a], array[b]] = [array[b], array[a]];
}
export function reverseCompare(compareFn) {
return (a, b) => compareFn(b, a);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
- Heap.js
import { Compare, defaultCompare, reverseCompare, swap } from '../util';
export class MinHeap {
constructor(compareFn = defaultCompare) {
this.compareFn = compareFn;
this.heap = [];
}
getLeftIndex(index) {
return (2 * index) + 1;
}
getRightIndex(index) {
return (2 * index) + 2;
}
getParentIndex(index) {
if (index === 0) {
return undefined;
}
return Math.floor((index - 1) / 2);
}
size() {
return this.heap.length;
}
isEmpty() {
return this.size() <= 0;
}
clear() {
this.heap = [];
}
findMinimum() {
return this.isEmpty() ? undefined : this.heap[0];
}
insert(value) {
if (value != null) {
const index = this.heap.length;
this.heap.push(value);
this.siftUp(index);
return true;
}
return false;
}
siftDown(index) {
let element = index;
const left = this.getLeftIndex(index);
const right = this.getRightIndex(index);
const size = this.size();
if (
left < size &&
this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN
) {
element = left;
}
if (
right < size &&
this.compareFn(this.heap[element], this.heap[right]) === Compare.BIGGER_THAN
) {
element = right;
}
if (index !== element) {
swap(this.heap, index, element);
this.siftDown(element);
}
}
siftUp(index) {
let parent = this.getParentIndex(index);
while (
index > 0 &&
this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN
) {
swap(this.heap, parent, index);
index = parent;
parent = this.getParentIndex(index);
}
}
extract() {
if (this.isEmpty()) {
return undefined;
}
if (this.size() === 1) {
return this.heap.shift();
}
const removedValue = this.heap[0];
this.heap[0] = this.heap.pop();
this.siftDown(0);
return removedValue;
}
heapify(array) {
if (array) {
this.heap = array;
}
const maxIndex = Math.floor(this.size() / 2) - 1;
for (let i = maxIndex; i >= 0; i--) {
this.siftDown(i);
}
return this.heap;
}
getAsArray() {
return this.heap;
}
}
export class MaxHeap extends MinHeap {
constructor(compareFn = defaultCompare) {
super(compareFn);
this.compareFn = compareFn;
this.compareFn = reverseCompare(compareFn);
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
- 使用MinHeap
let heap = new MinHeap();
heap.insert(2);
heap.insert(3);
heap.insert(4);
heap.insert(5);
heap.insert(2);
console.log(heap.getAsArray());
console.log('Heap size: ', heap.size()); // 5
console.log('Heap is empty: ', heap.isEmpty()); // false
console.log('Heap min value: ', heap.findMinimum()); // 1
heap = new MinHeap();
for (let i = 1; i < 10; i++) {
heap.insert(i);
}
console.log(heap.getAsArray());
console.log('Extract minimum: ', heap.extract()); // 1
console.log(heap.getAsArray()); // [2, 4, 3, 8, 5, 6, 7, 9]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- 使用MaxHeap
const maxHeap = new MaxHeap();
maxHeap.insert(2);
maxHeap.insert(3);
maxHeap.insert(4);
maxHeap.insert(5);
maxHeap.insert(1);
console.log(maxHeap.getAsArray());
console.log('Heap size: ', maxHeap.size()); // 5
console.log('Heap is empty: ', maxHeap.isEmpty()); // false
console.log('Heap min value: ', maxHeap.findMinimum()); // 5
maxHeap.insert(6);
maxHeap.insert(9);
maxHeap.insert(10);
maxHeap.insert(14);
console.log(maxHeap.getAsArray());
console.log('Extract minimum: ', maxHeap.extract());
console.log(maxHeap.getAsArray());
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24