数组排序
2021/6/18 array
# 冒泡排序
- 步骤
- 冒泡排序只会操作相邻的两个数据;
- 每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换;
- 一次冒泡会让至少一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作.
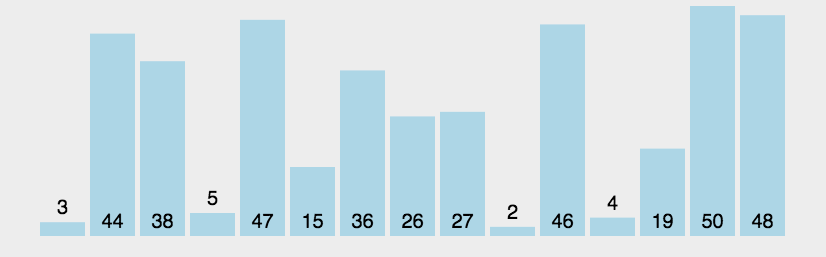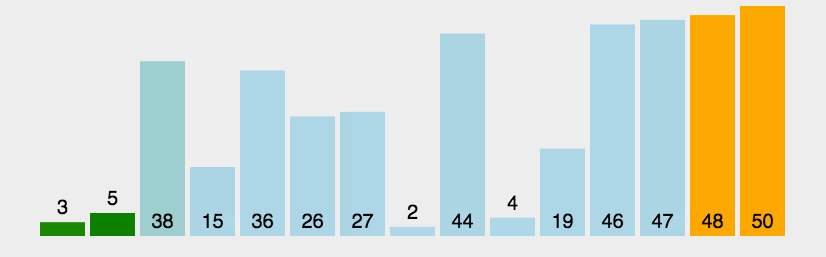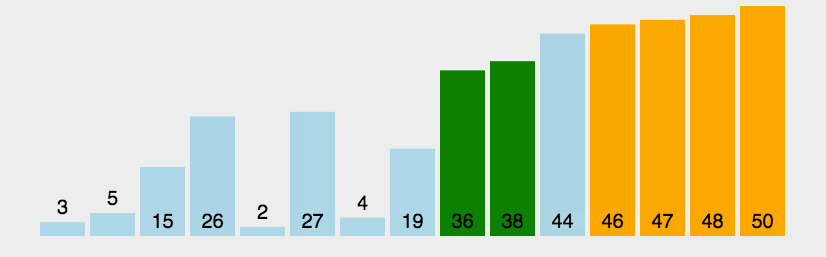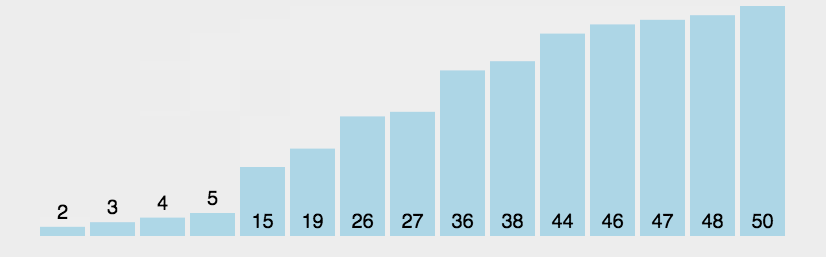
- 代码
function bubbleSort(arr) {
var i = arr.length - 1; //初始时,最后位置保持不变
while (i > 0) {
var pos = 0; //每趟开始时,无记录交换
for (var j = 0; j < i; j++)
console.log(arr[j], arr[j + 1])
if (arr[j] > arr[j + 1]) {
pos = j; //记录交换的位置
var tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
}
i = pos; //为下一趟排序作准备
}
return arr;
}
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(bubbleSort(arr));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 快速排序
相关资料: 资料 1 (opens new window) | 资料 2 (opens new window) | 资料 3 (opens new window) | 资料 4 (opens new window)
步骤
- 先找到一个基准点(一般指数组的中部),然后数组被该基准点分为两部分,依次与该基准点数据比较,如果比它小,放左边;反之,放右边。
- 左右分别用一个空数组去存储比较后的数据。
- 最后递归执行上述操作,直到
数组长度 <= 1
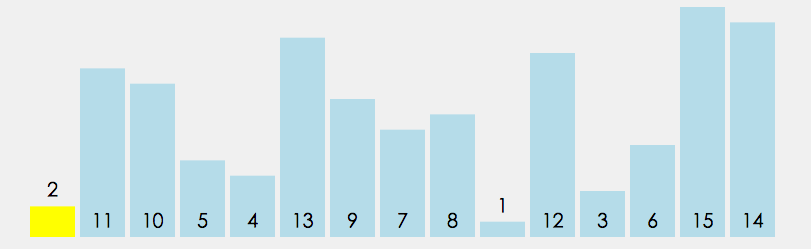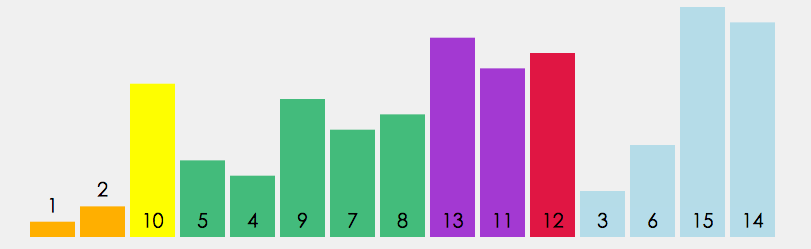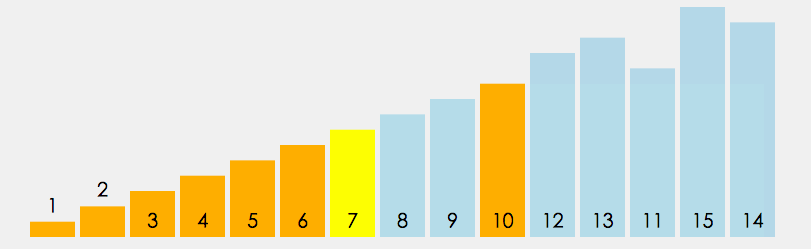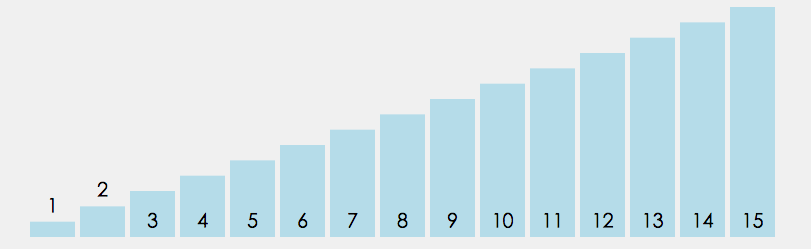
- 代码实现
const quickSort = nums => {
let arr = [...nums]
if (arr.length <= 1) {
return arr;
}
//取基准点
const midIndex = Math.floor(arr.length / 2);
//取基准点的值,splice(index,1) 则返回的是含有被删除的元素的数组。
const valArr = arr.splice(midIndex, 1);
const midIndexVal = valArr[0];
const left = []; //存放比基准点小的数组
const right = []; //存放比基准点大的数组
//遍历数组,进行判断分配
for (let i = 0; i < arr.length; i++) {
if (arr[i] < midIndexVal) {
left.push(arr[i]); //比基准点小的放在左边数组
} else {
right.push(arr[i]); //比基准点大的放在右边数组
}
}
//递归执行以上操作,对左右两个数组进行操作,直到数组长度为 <= 1
return quickSort(left).concat(midIndexVal, quickSort(right));
};
console.log('quickSort ', quickSort([5, 14, 3, 21, 10]));
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- 原地分区版快速排序实现
// 原地分区版快速排序实现
const quickSort2 = (arr, left, right) => {
let len = arr.length,
partitionIndex;
left = typeof left != 'number' ? 0 : left;
right = typeof right != 'number' ? len - 1 : right;
if (left < right) {
// 返回基准值的所在位置, 即索引
partitionIndex = partition(arr, left, right);
// 可理解为:把数组拆分为 左边的数组值都比基准值小,右边的数组都比基准值大
// 比对基准值左边的数组
quickSort2(arr, left, partitionIndex - 1);
// 比对基准值右边的数组
quickSort2(arr, partitionIndex + 1, right);
}
return arr;
};
const swap = (arr, i, j) => {
// let temp = arr[i];
// arr[i] = arr[j];
// arr[j] = temp;
[arr[i], arr[j]] = [arr[j], arr[i]]
};
const partition = (arr, left, right) => {
//分区操作
let pivotIdx = left, //基准值(pivot)的索引
pivot = arr[pivotIdx], // 基准值(pivot)
index = pivotIdx + 1; // 初始index的位置
// index: 最终记录着数组中首次比基准值(pivot)大的最后索引位置
// i 取 index 的下一个数与之对比
for (let i = index; i <= right; i++) {
// 判断基准值与当前项的大小
if (arr[i] < pivot) {
// 如果比基准值小,将arr[i] 与 arr[index]交换
// 即 小于基准值的 与 大于基准值的 互相交换
swap(arr, i, index);
// index 下移一位
index++;
}
}
// 将基准值与最后一次小于它的值交换
swap(arr, pivotIdx, index - 1);
// 返回最后一次比基准值小的索引位置: index-1
return index - 1;
};
const array2 = [8, 5, 1, 13, 2, 6, 9, 21];
console.log('quickSort2 ', quickSort2(array2));
// => [ 1, 2, 5, 6, 8, 9, 13, 21 ]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# 选择排序
- 步骤
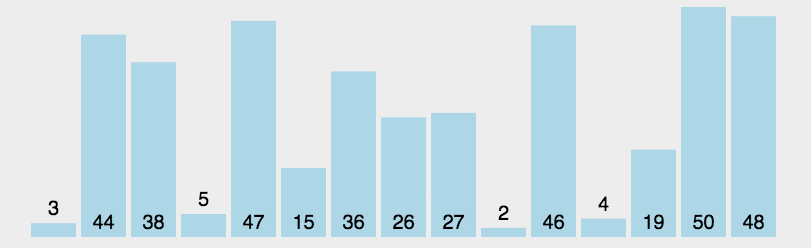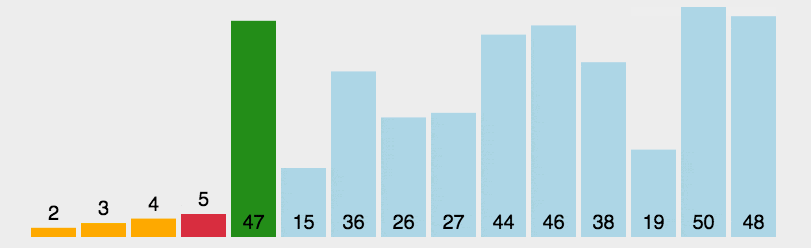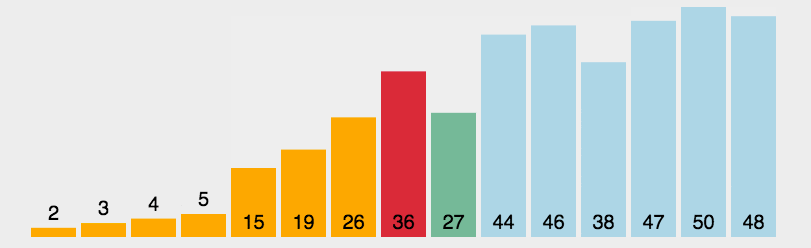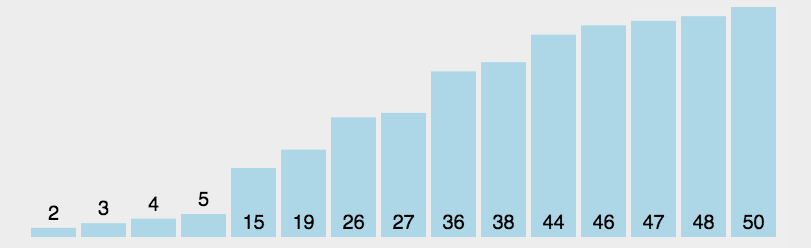
- 首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾
- 重复第二步,直到所有元素均排序完毕
- 代码
function selectionSort(arr) {
if (arr.length <= 1) return arr;
let len = arr.length;
let minIndex, temp;
for (let i = 0; i < len - 1; i++) {
minIndex = i;
for (let j = i + 1; j < len; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
// temp = arr[i];
// arr[i] = arr[minIndex];
// arr[minIndex] = temp;
}
return arr;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
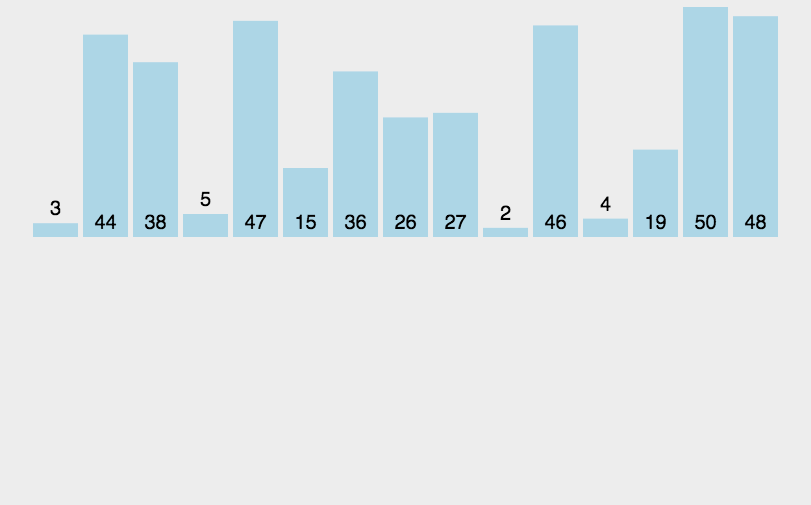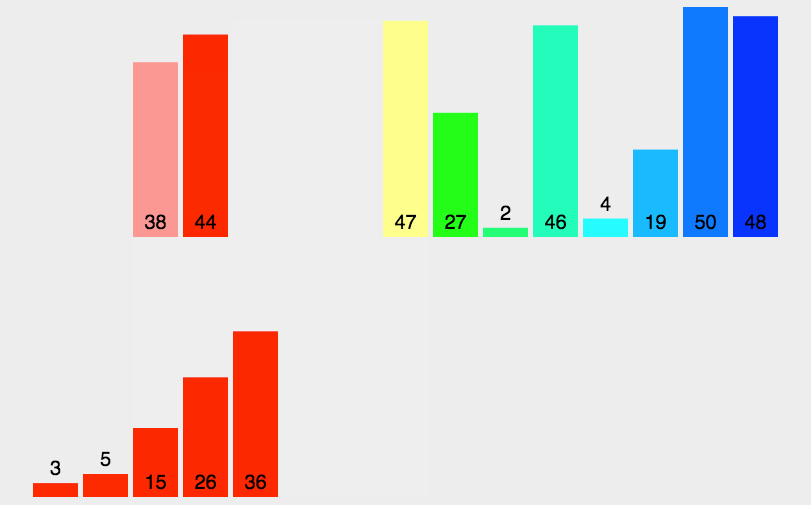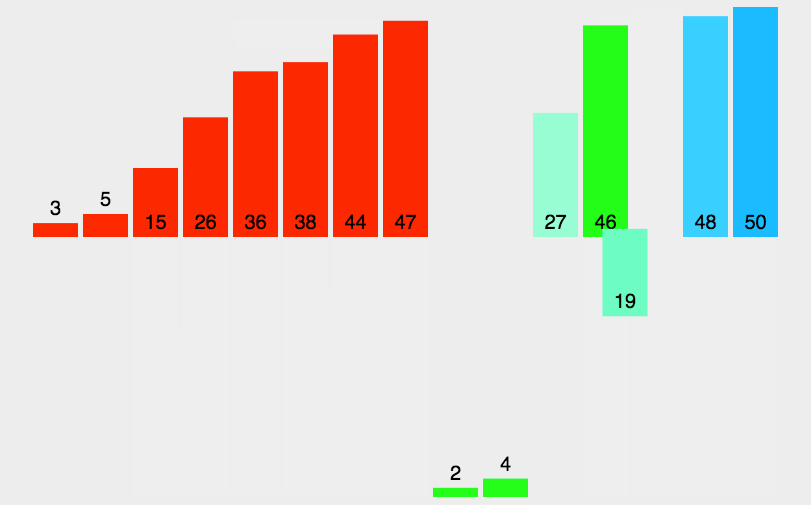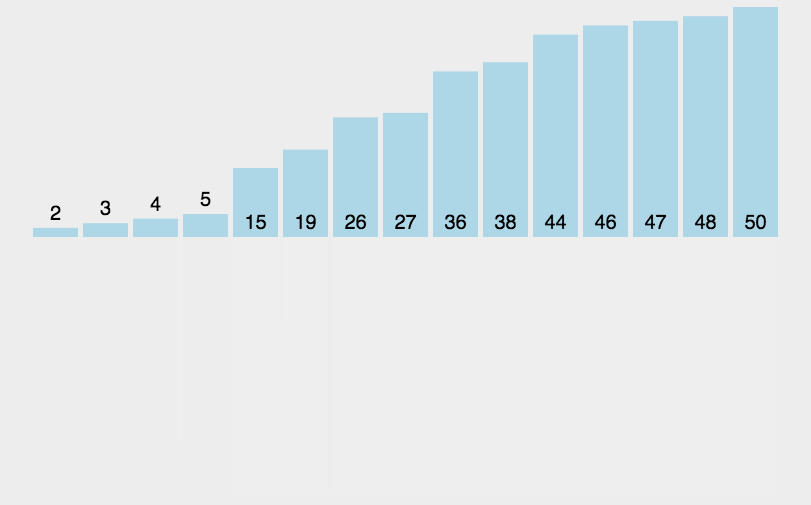
# 归并排序
排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序
- 代码
const mergeSort = arr => {
//采用自上而下的递归方法
const len = arr.length;
if (len < 2) {
return arr;
}
// length >> 1 和 Math.floor(len / 2) 等价
let middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle); // 拆分为两个子数组
return merge(mergeSort(left), mergeSort(right));
};
const merge = (left, right) => {
const result = [];
while (left.length && right.length) {
// 注意: 判断的条件是小于或等于,如果只是小于,那么排序将不稳定.
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length) result.push(left.shift());
while (right.length) result.push(right.shift());
return result;
};
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.time('归并排序耗时');
console.log('arr :', mergeSort(arr));
console.timeEnd('归并排序耗时');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 插入排序
# 直接插入
步骤
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤 3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤 2 ~ 5
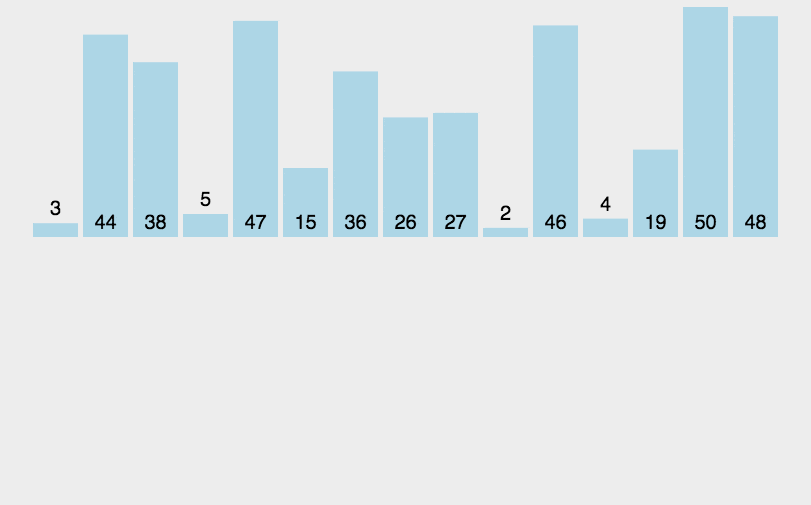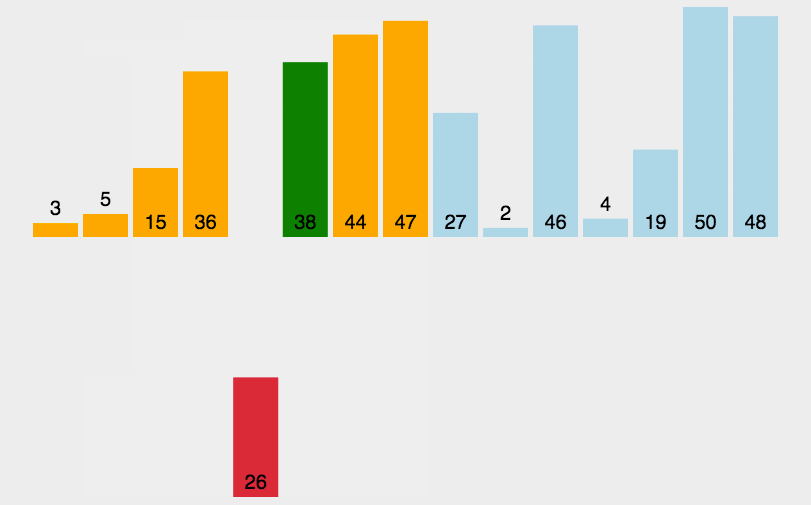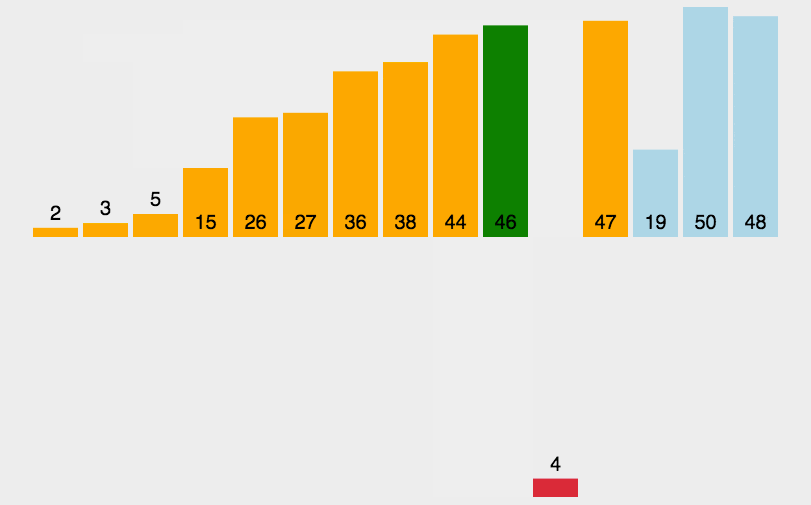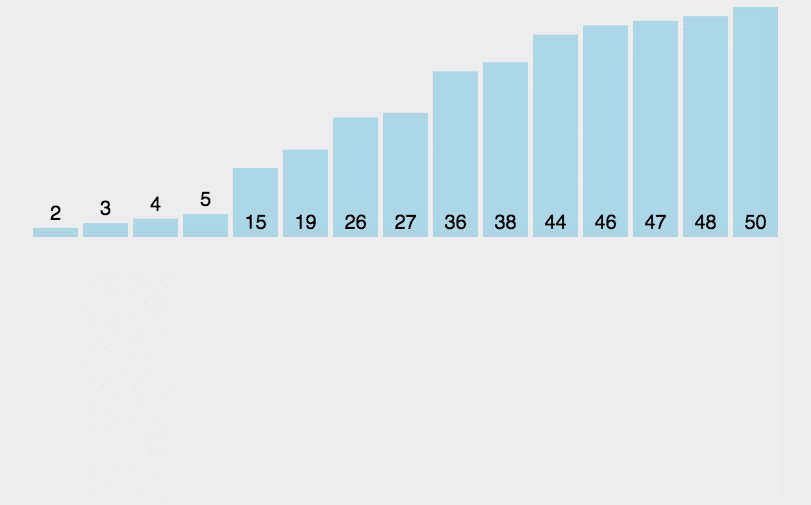
- 代码
// 插入排序
const insertionSort = array => {
const len = array.length;
if (len <= 1) return
let preIndex, current;
for (let i = 1; i < len; i++) {
preIndex = i - 1; //待比较元素的下标
current = array[i]; //当前元素
while (preIndex >= 0 && array[preIndex] > current) {
//前置条件之一: 待比较元素比当前元素大
array[preIndex + 1] = array[preIndex]; //将待比较元素后移一位
preIndex--; //游标前移一位
}
if (preIndex + 1 != i) {
//避免同一个元素赋值给自身
array[preIndex + 1] = current; //将当前元素插入预留空位
console.log('array :', array);
}
}
return array;
};
// 测试
const array = [5, 4, 3, 2, 1];
console.log("原始 array :", array);
insertionSort(array);
// 原始 array: [5, 4, 3, 2, 1]
// array: [4, 5, 3, 2, 1]
// array: [3, 4, 5, 2, 1]
// array: [2, 3, 4, 5, 1]
// array: [1, 2, 3, 4, 5]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 拆半插入
步骤
- 取
0 ~ i-1的中间点( m = (i-1) >> 1 ),array[i]与array[m]进行比较,若array[i] < array[m],则说明待插入的元素array[i]应该处于数组的0 ~ m索引之间;反之,则说明它应该处于数组的m ~ i-1索引之间。 - 重复步骤 1,每次缩小一半的查找范围,直至找到插入的位置。
- 将数组中插入位置之后的元素全部后移一位。
- 在指定位置插入第 i 个元素。
- 取
注:x >> 1 是位运算中的右移运算,表示右移一位,等同于 x 除以 2 再取整,即 x >> 1 == Math.floor(x/2)
- 代码
// 折半插入排序
const binaryInsertionSort = array => {
const len = array.length;
if (len <= 1) return;
let current, i, j, low, high, m;
for (i = 1; i < len; i++) {
low = 0;
high = i - 1;
current = array[i];
while (low <= high) {
//步骤 1 & 2 : 折半查找
m = (low + high) >> 1; // 注: x>>1 是位运算中的右移运算, 表示右移一位, 等同于 x 除以 2 再取整, 即 x>>1 == Math.floor(x/2) .
if (array[i] >= array[m]) {
//值相同时, 切换到高半区,保证稳定性
low = m + 1; //插入点在高半区
} else {
high = m - 1; //插入点在低半区
}
}
for (j = i; j > low; j--) {
//步骤 3: 插入位置之后的元素全部后移一位
array[j] = array[j - 1];
console.log('array2 :', JSON.parse(JSON.stringify(array)));
}
array[low] = current; //步骤 4: 插入该元素
}
console.log('array2 :', JSON.parse(JSON.stringify(array)));
return array;
};
const array2 = [5, 4, 3, 2, 1];
console.log('原始 array2:', array2);
binaryInsertionSort(array2);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# 希尔排序
- 步骤
- 先将整个待排序的记录序列分割成为若干子序列。
- 分别进行直接插入排序。
- 待整个序列中的记录基本有序时,再对全体记录进行依次直接插入排序。
- 代码
const shellSort = arr => {
let len = arr.length,
temp,
gap = 1;
console.time('希尔排序耗时');
while (gap < len / 3) {
//动态定义间隔序列
gap = gap * 3 + 1;
}
for (gap; gap > 0; gap = Math.floor(gap / 3)) {
for (let i = gap; i < len; i++) {
temp = arr[i];
let j = i - gap;
for (; j >= 0 && arr[j] > temp; j -= gap) {
arr[j + gap] = arr[j];
}
arr[j + gap] = temp;
console.log('arr :', arr);
}
}
console.timeEnd('希尔排序耗时');
return arr;
};
// 测试
const array = [35, 33, 42, 10, 14, 19, 27, 44];
console.log('原始array:', array);
const newArr = shellSort(array);
console.log('newArr:', newArr);
// 原始 array: [35, 33, 42, 10, 14, 19, 27, 44]
// arr : [14, 33, 42, 10, 35, 19, 27, 44]
// arr : [14, 19, 42, 10, 35, 33, 27, 44]
// arr : [14, 19, 27, 10, 35, 33, 42, 44]
// arr : [14, 19, 27, 10, 35, 33, 42, 44]
// arr : [14, 19, 27, 10, 35, 33, 42, 44]
// arr : [14, 19, 27, 10, 35, 33, 42, 44]
// arr : [10, 14, 19, 27, 35, 33, 42, 44]
// arr : [10, 14, 19, 27, 35, 33, 42, 44]
// arr : [10, 14, 19, 27, 33, 35, 42, 44]
// arr : [10, 14, 19, 27, 33, 35, 42, 44]
// arr : [10, 14, 19, 27, 33, 35, 42, 44]
// 希尔排序耗时: 3.592041015625ms
// newArr: [10, 14, 19, 27, 33, 35, 42, 44]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# 堆排序
- 代码
// 堆排序
const heapSort = array => {
console.time('堆排序耗时');
// 初始化大顶堆,从第一个非叶子结点开始
for (let i = Math.floor(array.length / 2 - 1); i >= 0; i--) {
heapify(array, i, array.length);
}
// 排序,每一次 for 循环找出一个当前最大值,数组长度减一
for (let i = Math.floor(array.length - 1); i > 0; i--) {
// 根节点与最后一个节点交换
swap(array, 0, i);
// 从根节点开始调整,并且最后一个结点已经为当前最大值,不需要再参与比较,所以第三个参数为 i,即比较到最后一个结点前一个即可
heapify(array, 0, i);
}
console.timeEnd('堆排序耗时');
return array;
};
// 交换两个节点
const swap = (array, i, j) => {
let temp = array[i];
array[i] = array[j];
array[j] = temp;
};
// 将 i 结点以下的堆整理为大顶堆,注意这一步实现的基础实际上是:
// 假设结点 i 以下的子堆已经是一个大顶堆,heapify 函数实现的
// 功能是实际上是:找到 结点 i 在包括结点 i 的堆中的正确位置。
// 后面将写一个 for 循环,从第一个非叶子结点开始,对每一个非叶子结点
// 都执行 heapify 操作,所以就满足了结点 i 以下的子堆已经是一大顶堆
const heapify = (array, i, length) => {
let temp = array[i]; // 当前父节点
// j < length 的目的是对结点 i 以下的结点全部做顺序调整
for (let j = 2 * i + 1; j < length; j = 2 * j + 1) {
temp = array[i]; // 将 array[i] 取出,整个过程相当于找到 array[i] 应处于的位置
if (j + 1 < length && array[j] < array[j + 1]) {
j++; // 找到两个孩子中较大的一个,再与父节点比较
}
if (temp < array[j]) {
swap(array, i, j); // 如果父节点小于子节点:交换;否则跳出
i = j; // 交换后,temp 的下标变为 j
} else {
break;
}
}
};
// 测试
const array = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
console.log('原始array:', array);
const newArr = heapSort(array);
console.log('newArr:', newArr);
// 原始 array: [4, 6, 8, 5, 9, 1, 2, 5, 3, 2]
// 堆排序耗时: 0.15087890625ms
// newArr: [1, 2, 2, 3, 4, 5, 5, 6, 8, 9]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# 桶排序
- 代码
// 桶排序
const bucketSort = (array, bucketSize) => {
if (array.length === 0) {
return array;
}
console.time('桶排序耗时');
let i = 0;
let minValue = array[0];
let maxValue = array[0];
for (i = 1; i < array.length; i++) {
if (array[i] < minValue) {
minValue = array[i]; //输入数据的最小值
} else if (array[i] > maxValue) {
maxValue = array[i]; //输入数据的最大值
}
}
//桶的初始化
const DEFAULT_BUCKET_SIZE = 5; //设置桶的默认数量为 5
bucketSize = bucketSize || DEFAULT_BUCKET_SIZE;
const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
const buckets = new Array(bucketCount);
for (i = 0; i < buckets.length; i++) {
buckets[i] = [];
}
//利用映射函数将数据分配到各个桶中
for (i = 0; i < array.length; i++) {
buckets[Math.floor((array[i] - minValue) / bucketSize)].push(array[i]);
}
array.length = 0;
for (i = 0; i < buckets.length; i++) {
quickSort(buckets[i]); //对每个桶进行排序,这里使用了快速排序
for (var j = 0; j < buckets[i].length; j++) {
array.push(buckets[i][j]);
}
}
console.timeEnd('桶排序耗时');
return array;
};
// 快速排序
const quickSort = (arr, left, right) => {
let len = arr.length,
partitionIndex;
left = typeof left != 'number' ? 0 : left;
right = typeof right != 'number' ? len - 1 : right;
if (left < right) {
partitionIndex = partition(arr, left, right);
quickSort(arr, left, partitionIndex - 1);
quickSort(arr, partitionIndex + 1, right);
}
return arr;
};
const partition = (arr, left, right) => {
//分区操作
let pivot = left, //设定基准值(pivot)
index = pivot + 1;
for (let i = index; i <= right; i++) {
if (arr[i] < arr[pivot]) {
swap(arr, i, index);
index++;
}
}
swap(arr, pivot, index - 1);
return index - 1;
};
const swap = (arr, i, j) => {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
};
// 测试
const array = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
console.log('原始array:', array);
const newArr = bucketSort(array);
console.log('newArr:', newArr);
// 原始 array: [4, 6, 8, 5, 9, 1, 2, 5, 3, 2]
// 堆排序耗时: 0.133056640625ms
// newArr: [1, 2, 2, 3, 4, 5, 5, 6, 8, 9]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
# 计数排序
- 代码
const countingSort = array => {
let len = array.length,
result = [],
countArr = [],
min = (max = array[0]);
console.time('计数排序耗时');
for (let i = 0; i < len; i++) {
// 获取最小,最大 值
min = min <= array[i] ? min : array[i];
max = max >= array[i] ? max : array[i];
countArr[array[i]] = countArr[array[i]] ? countArr[array[i]] + 1 : 1;
}
console.log('countArr :', countArr);
// 从最小值 -> 最大值,将计数逐项相加
for (let j = min; j < max; j++) {
countArr[j + 1] = (countArr[j + 1] || 0) + (countArr[j] || 0);
}
console.log('countArr 2:', countArr);
// countArr 中,下标为 array 数值,数据为 array 数值出现次数;反向填充数据进入 result 数据
for (let k = len - 1; k >= 0; k--) {
// result[位置] = array 数据
result[countArr[array[k]] - 1] = array[k];
// 减少 countArr 数组中保存的计数
countArr[array[k]]--;
// console.log("array[k]:", array[k], 'countArr[array[k]] :', countArr[array[k]],)
console.log('result:', result);
}
console.timeEnd('计数排序耗时');
return result;
};
// 测试
const array = [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];
console.log('原始 array: ', array);
const newArr = countingSort(array);
console.log('newArr: ', newArr);
// 原始 array: [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2]
// 计数排序耗时: 5.6708984375ms
// newArr: [1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# 基数排序
- 代码
/**
* name: 基数排序
* @param array 待排序数组
* @param max 最大位数
*/
const radixSort = (array, max) => {
console.time('计数排序耗时');
const buckets = [];
let unit = 10,
base = 1;
for (let i = 0; i < max; i++ , base *= 10, unit *= 10) {
for (let j = 0; j < array.length; j++) {
let index = ~~((array[j] % unit) / base); //依次过滤出个位,十位等等数字
if (buckets[index] == null) {
buckets[index] = []; //初始化桶
}
buckets[index].push(array[j]); //往不同桶里添加数据
}
let pos = 0,
value;
for (let j = 0, length = buckets.length; j < length; j++) {
if (buckets[j] != null) {
while ((value = buckets[j].shift()) != null) {
array[pos++] = value; //将不同桶里数据挨个捞出来,为下一轮高位排序做准备,由于靠近桶底的元素排名靠前,因此从桶底先捞
}
}
}
}
console.timeEnd('计数排序耗时');
return array;
};
// 测试
const array = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log('原始array:', array);
const newArr = radixSort(array, 2);
console.log('newArr:', newArr);
// 原始 array: [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
// 堆排序耗时: 0.064208984375ms
// newArr: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 算法可视化工具
# 二分查找(Binary Search)
二分查找,前提是数组为有序数组, 返回索引值, O(㏒n)复杂度
var search = function(nums, target){
let left = 0, right = nums.length - 1;
while(left <= right){
const mid = Math.floor((right-left)/2 + left)
const midVal = nums[mid]
if(midVal == target){
return mid
}else if(midVal > target){
right = mid - 1
}else{
left = mid + 1
}
}
return -1
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 搜索插入位置
var searchInsert = function(nums, target) {
const len = nums.length;
let left = 0, right=len-1, index = len;
while(left <= right){
let mid = Math.floor((right - left) /2 + left)
if(target <= nums[mid]){
index = mid;
right = mid - 1;
}else{
left = mid + 1;
}
}
return index
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 有序数组合并为一个数组
function mergeArray (left, right) {
let result = [],
il = 0,
ir = 0;
while(il < left.length && ir < right.length) {
if (left[il] < right[ir]) {
result.push(left[il++]);
} else {
result.push(right[ir++]);
}
}
return result.concat(left[il] ? left.slice(il) : right.slice(ir));
}
mergeArray([2,4,5], [1,3,6])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var merge = function(nums1, m, nums2, n) {
// 初始化两个指针的指向,初始化 nums1 尾部索引k
let i = m - 1, j = n - 1, k = m + n - 1
// 当两个数组都没遍历完时,指针同步移动
while(i >= 0 && j >= 0) {
// 取较大的值,从末尾往前填补
if(nums1[i] >= nums2[j]) {
nums1[k] = nums1[i] // <-
i--
k--
} else {
nums1[k] = nums2[j]
j--
k--
}
}
// nums2 留下的情况,特殊处理一下
while(j>=0) {
nums1[k] = nums2[j]
k--
j--
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 数组去重
- 方法1
function unique(arr) {
var result = [];
for (var i = 0, len = arr.length; i < len; i++) {
var arri = arr[i];
if (result.indexOf(arri) < 0) {
result.push(arri);
}
}
return result;
}
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
- 方法2
function unique(arr) {
for (let i = 0, len = arr.length; i < len; i++) {
for (let j = i + 1; j < len; j++) {
if (arr[i] == arr[j]) {
arr.splice(j, 1)
len--;
j--
}
}
}
return arr
}
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
- 方法3
function unique(arr) {
return arr.filter((item, index) => {
return arr.indexOf(item) === index
})
}
1
2
3
4
5
2
3
4
5
- 方法4
function unique(arr) {
return [...new Set(arr)]
}
1
2
3
2
3
